Building a DeepGraph of Extreme Precipitation¶
[ipython notebook] [python script] [data]
In the following we build a deep graph of a high-resolution dataset of precipitation measurements.
The goal is to first detect spatiotemporal clusters of extreme precipitation events and then to create families of these clusters based on a spatial correlation measure. Finally, we create and plot some informative (intersection) partitions of the deep graph.
For further details see section V of the original paper: https://arxiv.org/abs/1604.00971
First of all, we need to import some packages
# data i/o
import os
import xarray
# for plots
import matplotlib.pyplot as plt
# the usual
import numpy as np
import pandas as pd
import deepgraph as dg
# notebook display
from IPython.display import HTML
%matplotlib inline
plt.rcParams['figure.figsize'] = 8, 6
pd.options.display.max_rows = 10
pd.set_option('expand_frame_repr', False)
Selecting and Preprocessing the Precipitation Data¶
Selection¶
If you want to select your own spatiotemporal box of precipitation events, you may follow the instructions below and change the filename in the next box of code.
- Go to https://disc.gsfc.nasa.gov/datasets/TRMM_3B42_V7/summary?keywords=TRMM_3B42_V7
- click on “Simple Subset Wizard”
- select the “Date Range” (and if desired a “Spatial Bounding Box”) you’re interested in
- click on “Search for Data Sets”
- expand the list by clicking on the “+” symbol
- mark the check box “precipitation”
- (optional, but recommended) click on the selector to change from “netCDF” to “gzipped netCDF”
- click on “Subset Selected Data Sets”
- click on “View Subset Results”
- right click on the “Get list of URLs for this subset in a file” link, and choose “Save Link As…”
- the downloaded file will have a name similar to “SSW_download_2016-05-03T20_19_28_23621_2oIe06xp.inp”. Note which directory the downloaded file is saved to, and in your Unix shell, set your current working directory to that directory.
- register an account to get authentication credentials using these instructions: https://disc.gsfc.nasa.gov/information/howto/5761bc6a5ad5a18811681bae?keywords=wget
- get the files via
os.system("wget --content-disposition --directory-prefix=tmp --load-cookies ~/.urs_cookies --save-cookies ~/.urs_cookies --auth-no-challenge=on --keep-session-cookies -i SSW_download_2016-05-03T20_19_28_23621_2oIe06xp.inp")
Preprocessing¶
Next, we need to convert the downloaded netCDF files to a pandas DataFrame, which we can then use to initiate a dg.DeepGraph
# choose "wet times" threshold
r = .1
# choose "extreme" precipitation threshold
p = .9
v_list = []
for file in os.listdir('tmp'):
if file.startswith('3B42.'):
# open the downloaded netCDF file
# unfortunately, we have to decode times ourselves, since
# the format of the downloaded files doesn't work
# see also: https://github.com/pydata/xarray/issues/521
f = xarray.open_dataset('tmp/{}'.format(file), decode_times=False)
# create integer-based (x,y) coordinates
f['x'] = (('longitude'), np.arange(len(f.longitude)))
f['y'] = (('latitude'), np.arange(len(f.latitude)))
# convert to pd.DataFrame
vt = f.to_dataframe()
# we only consider "wet times", pcp >= 0.1mm/h
vt = vt[vt.pcp >= r]
# reset index
vt.reset_index(inplace=True)
# add correct times
ftime = f.time.units.split()[2:]
year, month, day = ftime[0].split('-')
hour = ftime[1]
time = pd.datetime(int(year), int(month), int(day), int(hour))
vt['time'] = time
# compute "area" for each event
vt['area'] = 111**2 * .25**2 * np.cos(2*np.pi*vt.latitude / 360.)
# compute "volume of water precipitated" for each event
vt['vol'] = vt.pcp * 3 * vt.area
# set dtypes -> economize ram
vt['pcp'] = vt['pcp'] * 100
vt['pcp'] = vt['pcp'].astype(np.uint16)
vt['latitude'] = vt['latitude'].astype(np.float16)
vt['longitude'] = vt['longitude'].astype(np.float16)
vt['area'] = vt['area'].astype(np.uint16)
vt['vol'] = vt['vol'].astype(np.uint32)
vt['x'] = vt['x'].astype(np.uint16)
vt['y'] = vt['y'].astype(np.uint16)
# append to list
v_list.append(vt)
f.close()
# concatenate the DataFrames
v = pd.concat(v_list)
# append a column indicating geographical locations (i.e., supernode labels)
v['g_id'] = v.groupby(['longitude', 'latitude']).grouper.group_info[0]
v['g_id'] = v['g_id'].astype(np.uint32)
# select `p`th percentile of precipitation events for each geographical location
v = v.groupby('g_id').apply(lambda x: x[x.pcp >= x.pcp.quantile(p)])
# append integer-based time
dtimes = pd.date_range(v.time.min(), v.time.max(), freq='3H')
dtdic = {dtime: itime for itime, dtime in enumerate(dtimes)}
v['itime'] = v.time.apply(lambda x: dtdic[x])
v['itime'] = v['itime'].astype(np.uint16)
# sort by time
v.sort_values('time', inplace=True)
# set unique node index
v.set_index(np.arange(len(v)), inplace=True)
# shorten column names
v.rename(columns={'pcp': 'r',
'latitude': 'lat',
'longitude': 'lon',
'time': 'dtime',
'itime': 'time'},
inplace=True)
The created DataFrame of extreme precipitation measurements looks like this
print(v)
lat lon dtime r x y area vol g_id time
0 15.125 -118.125 2004-08-20 1084 28 101 743 24174 5652 0
1 44.875 -30.625 2004-08-20 392 378 220 545 6433 85341 0
2 45.125 -30.625 2004-08-20 454 378 221 543 7416 85342 0
3 45.375 -30.625 2004-08-20 909 378 222 540 14767 85343 0
4 45.625 -30.625 2004-08-20 907 378 223 538 14669 85344 0
... ... ... ... ... ... ... ... ... ... ...
382306 26.875 -46.625 2004-09-27 503 314 148 686 10385 70380 304
382307 38.375 -37.125 2004-09-27 453 352 194 603 8222 79095 304
382308 8.125 -105.125 2004-09-27 509 80 73 762 11663 17007 304
382309 21.875 -42.875 2004-09-27 260 329 128 714 5595 73875 304
382310 6.625 -111.125 2004-09-27 192 56 67 764 4428 11790 304
[382311 rows x 10 columns]
We identify each row of this table as a node of our DeepGraph
g = dg.DeepGraph(v)
Plot the Data¶
Let’s take a look at the data by creating a video of the time-evolution of precipitation measurements. Using the plot_map_generator method, this is straight forward.
# configure map projection
kwds_basemap = {'llcrnrlon': v.lon.min() - 1,
'urcrnrlon': v.lon.max() + 1,
'llcrnrlat': v.lat.min() - 1,
'urcrnrlat': v.lat.max() + 1,
'resolution': 'i'}
# configure scatter plots
kwds_scatter = {'s': 1.5,
'c': g.v.r.values / 100.,
'edgecolors': 'none',
'cmap': 'viridis_r'}
# create generator of scatter plots on map
objs = g.plot_map_generator('lon', 'lat', 'dtime',
kwds_basemap=kwds_basemap,
kwds_scatter=kwds_scatter)
# plot and store frames
for i, obj in enumerate(objs):
# configure plots
cb = obj['fig'].colorbar(obj['pc'], fraction=0.025, pad=0.01)
cb.set_label('[mm/h]')
obj['m'].fillcontinents(color='0.2', zorder=0, alpha=.4)
obj['ax'].set_title('{}'.format(obj['group']))
# store and close
obj['fig'].savefig('tmp/pcp_{:03d}.png'.format(i),
dpi=300, bbox_inches='tight')
plt.close(obj['fig'])
# create video with ffmpeg
cmd = "ffmpeg -y -r 5 -i tmp/pcp_%03d.png -c:v libx264 -r 20 -vf scale=2052:1004 {}.mp4"
os.system(cmd.format('precipitation_files/pcp'))
# embed video
HTML("""
<video width="700" height="350" controls>
<source src="precipitation_files/pcp.mp4" type="video/mp4">
</video>
""")
Detecting SpatioTemporal Clusters of Extreme Precipitation¶
In this tutorial, we’re interested in local formations of spatiotemporal clusters of extreme precipitation events. For that matter, we now use DeepGraph to identify such clusters and track their temporal evolution.
Create Edges¶
We now use DeepGraph to create edges between the nodes given by g.v.
The edges of g will be utilized to detect spatiotemporal clusters in
the data, or in more technical terms: to partition the set of all nodes
into subsets of connected grid points. One can imagine the nodes to be
elements of a \(3\) dimensional grid box (x,y,time), where we allow
every node to have \(26\) possible neighbours (\(8\) neighbours
in the time slice of the measurement, \(t_i\), and \(9\)
neighbours in each the time slice \(t_i − 1\) and \(t_i + 1\)).
For that matter, we pass the following connectors
def grid_2d_dx(x_s, x_t):
dx = x_t - x_s
return dx
def grid_2d_dy(y_s, y_t):
dy = y_t - y_s
return dy
and selectors
def s_grid_2d_dx(dx, sources, targets):
dxa = np.abs(dx)
sources = sources[dxa <= 1]
targets = targets[dxa <= 1]
return sources, targets
def s_grid_2d_dy(dy, sources, targets):
dya = np.abs(dy)
sources = sources[dya <= 1]
targets = targets[dya <= 1]
return sources, targets
to the create_edges_ft method
g.create_edges_ft(ft_feature=('time', 1),
connectors=[grid_2d_dx, grid_2d_dy],
selectors=[s_grid_2d_dx, s_grid_2d_dy],
r_dtype_dic={'ft_r': np.bool,
'dx': np.int8,
'dy': np.int8},
logfile='create_e',
max_pairs=1e7)
# rename fast track relation
g.e.rename(columns={'ft_r': 'dt'}, inplace=True)
To see how many nodes and edges our graph’s comprised of, one may simply type
g
<DeepGraph object, with n=382311 node(s) and m=567225 edge(s) at 0x7f7a4c3de160>
The edges we just created look like this
print(g.e)
dx dy dt
s t
0 1362 0 1 False
1432 1 0 False
1433 1 1 False
1696 1 0 True
1699 1 1 True
... .. .. ...
382284 382291 0 1 False
382295 382296 0 1 False
382296 382299 0 1 False
382299 382309 0 1 False
382304 382306 0 1 False
[567225 rows x 3 columns]
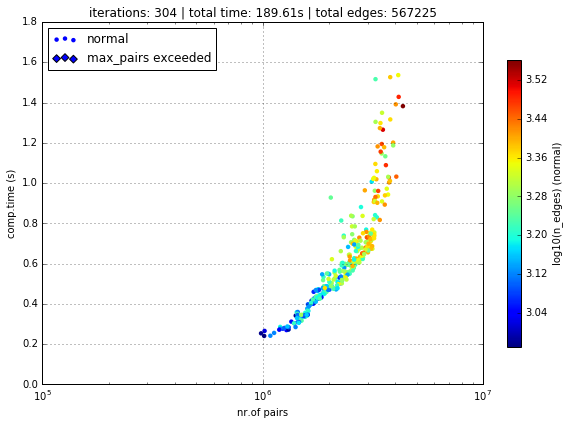
Logfile Plot
To see how long it took to create the edges, one may use the plot_logfile method
g.plot_logfile('create_e')
Find the Connected Components¶
Having linked all neighbouring nodes, the spatiotemporal clusters can be identified as the connected components of the graph. For practical reasons, DeepGraph directly implements a method to find the connected components of a graph, append_cp
# all singular components (components comprised of one node only)
# are consolidated under the label 0
g.append_cp(consolidate_singles=True)
# we don't need the edges any more
del g.e
the node table now has a component membership column appended
print(g.v)
lat lon dtime r x y area vol g_id time cp
0 15.125 -118.125 2004-08-20 1084 28 101 743 24174 5652 0 865
1 44.875 -30.625 2004-08-20 392 378 220 545 6433 85341 0 5079
2 45.125 -30.625 2004-08-20 454 378 221 543 7416 85342 0 5079
3 45.375 -30.625 2004-08-20 909 378 222 540 14767 85343 0 5079
4 45.625 -30.625 2004-08-20 907 378 223 538 14669 85344 0 5079
... ... ... ... ... ... ... ... ... ... ... ...
382306 26.875 -46.625 2004-09-27 503 314 148 686 10385 70380 304 609
382307 38.375 -37.125 2004-09-27 453 352 194 603 8222 79095 304 0
382308 8.125 -105.125 2004-09-27 509 80 73 762 11663 17007 304 174
382309 21.875 -42.875 2004-09-27 260 329 128 714 5595 73875 304 8
382310 6.625 -111.125 2004-09-27 192 56 67 764 4428 11790 304 15610
[382311 rows x 11 columns]
Let’s see how many spatiotemporal clusters g is comprised of
(discarding singular components)
g.v.cp.max()
33169
and how many nodes there are in the components
print(g.v.cp.value_counts())
0 64678
1 16460
2 8519
3 6381
4 3403
...
29601 2
27554 2
25507 2
23460 2
20159 2
Name: cp, dtype: int64
Partition the Nodes Into a Component Supernode Table¶
In order to aggregate and compute some information about the precipitiation clusters, we now partition the nodes by the type of feature cp, the component membership labels of the nodes just created. This can be done with the partition_nodes method
# feature functions, will be applied to each component of g
feature_funcs = {'dtime': [np.min, np.max],
'time': [np.min, np.max],
'vol': [np.sum],
'lat': [np.mean],
'lon': [np.mean]}
# partition the node table
cpv, gv = g.partition_nodes('cp', feature_funcs, return_gv=True)
# append geographical id sets
cpv['g_ids'] = gv['g_id'].apply(set)
# append cardinality of g_id sets
cpv['n_unique_g_ids'] = cpv['g_ids'].apply(len)
# append time spans
cpv['dt'] = cpv['dtime_amax'] - cpv['dtime_amin']
# append spatial coverage
def area(group):
return group.drop_duplicates('g_id').area.sum()
cpv['area'] = gv.apply(area)
The clusters look like this
print(cpv)
n_nodes dtime_amin dtime_amax time_amin time_amax lat_mean vol_sum lon_mean g_ids n_unique_g_ids dt area
cp
0 64678 2004-08-20 00:00:00 2004-09-27 00:00:00 0 304 17.609375 627097323 -63.40625 {0, 1, 2, 6, 7, 10, 12, 13, 14, 22, 23, 24, 25... 49808 38 days 00:00:00 34781178
1 16460 2004-09-01 06:00:00 2004-09-17 18:00:00 98 230 17.281250 351187150 -65.12500 {65536, 65537, 65538, 65539, 65540, 65541, 655... 6629 16 days 12:00:00 4803624
2 8519 2004-09-17 03:00:00 2004-09-24 15:00:00 225 285 26.906250 133698579 -44.62500 {73728, 73729, 73730, 73731, 73732, 73733, 737... 3730 7 days 12:00:00 2507350
3 6381 2004-08-26 09:00:00 2004-09-06 03:00:00 51 137 21.062500 113782748 -64.12500 {65555, 65556, 65557, 65558, 65559, 65560, 655... 2442 10 days 18:00:00 1749673
4 3403 2004-08-21 21:00:00 2004-08-24 12:00:00 15 36 10.578125 66675326 -111.93750 {8141, 14654, 11805, 16363, 8142, 11806, 20490... 1294 2 days 15:00:00 978604
... ... ... ... ... ... ... ... ... ... ... ... ...
33165 2 2004-08-23 18:00:00 2004-08-23 18:00:00 30 30 15.500000 20212 -103.87500 {18115, 18116} 2 0 days 00:00:00 1483
33166 2 2004-09-05 18:00:00 2004-09-05 18:00:00 134 134 27.250000 9366 -121.87500 {2688, 2687} 2 0 days 00:00:00 1368
33167 2 2004-08-30 15:00:00 2004-08-30 15:00:00 85 85 9.250000 43096 0.62500 {112116, 112117} 2 0 days 00:00:00 1519
33168 2 2004-09-09 03:00:00 2004-09-09 03:00:00 161 161 6.750000 24156 -13.62500 {100613, 100614} 2 0 days 00:00:00 1528
33169 2 2004-09-11 03:00:00 2004-09-11 03:00:00 177 177 15.500000 46798 -16.12500 {98523, 98524} 2 0 days 00:00:00 1483
[33170 rows x 12 columns]
Plot the Largest Component¶
Let’s see how the largest cluster of extreme precipitation evolves over time, again using the plot_map_generator method
# temporary DeepGraph instance containing
# only the largest component
gt = dg.DeepGraph(g.v)
gt.filter_by_values_v('cp', 1)
# configure map projection
from mpl_toolkits.basemap import Basemap
m1 = Basemap(projection='ortho',
lon_0=cpv.loc[1].lon_mean + 12,
lat_0=cpv.loc[1].lat_mean + 8,
resolution=None)
width = (m1.urcrnrx - m1.llcrnrx) * .65
height = (m1.urcrnry - m1.llcrnry) * .45
kwds_basemap = {'projection': 'ortho',
'lon_0': cpv.loc[1].lon_mean + 12,
'lat_0': cpv.loc[1].lat_mean + 8,
'llcrnrx': -0.5 * width,
'llcrnry': -0.5 * height,
'urcrnrx': 0.5 * width,
'urcrnry': 0.5 * height,
'resolution': 'i'}
# configure scatter plots
kwds_scatter = {'s': 2,
'c': np.log(gt.v.r.values / 100.),
'edgecolors': 'none',
'cmap': 'viridis_r'}
# create generator of scatter plots on map
objs = gt.plot_map_generator('lon', 'lat', 'dtime',
kwds_basemap=kwds_basemap,
kwds_scatter=kwds_scatter)
# plot and store frames
for i, obj in enumerate(objs):
# configure plots
obj['m'].fillcontinents(color='0.2', zorder=0, alpha=.4)
obj['m'].drawparallels(range(-50, 50, 20), linewidth=.2)
obj['m'].drawmeridians(range(0, 360, 20), linewidth=.2)
obj['ax'].set_title('{}'.format(obj['group']))
# store and close
obj['fig'].savefig('tmp/cp1_ortho_{:03d}.png'.format(i),
dpi=300, bbox_inches='tight')
plt.close(obj['fig'])
# create video with ffmpeg
cmd = "ffmpeg -y -r 5 -i tmp/cp1_ortho_%03d.png -c:v libx264 -r 20 -vf scale=1919:1406 {}.mp4"
os.system(cmd.format('precipitation_files/cp1_ortho'))
# embed video
HTML("""
<video width="700" height="500" controls>
<source src="precipitation_files/cp1_ortho.mp4" type="video/mp4">
</video>
""")
Detecting Families of Spatially Related Clusters¶
Create SuperEdges between the Components¶
We now create superedges between the spatiotemporal clusters in order to find families of clusters that have a strong regional overlap. Passing the following connectors and selector
# compute intersection of geographical locations
def cp_node_intersection(g_ids_s, g_ids_t):
intsec = np.zeros(len(g_ids_s), dtype=object)
intsec_card = np.zeros(len(g_ids_s), dtype=np.int)
for i in range(len(g_ids_s)):
intsec[i] = g_ids_s[i].intersection(g_ids_t[i])
intsec_card[i] = len(intsec[i])
return intsec_card
# compute a spatial overlap measure between clusters
def cp_intersection_strength(n_unique_g_ids_s, n_unique_g_ids_t, intsec_card):
min_card = np.array(np.vstack((n_unique_g_ids_s, n_unique_g_ids_t)).min(axis=0),
dtype=np.float64)
intsec_strength = intsec_card / min_card
return intsec_strength
# compute temporal distance between clusters
def time_dist(dtime_amin_s, dtime_amin_t):
dt = dtime_amin_t - dtime_amin_s
return dt
to the create_edges method will provide the information necessary for this task
# discard singular components
cpv.drop(0, inplace=True)
# we only consider the largest 5000 clusters
cpv = cpv.iloc[:5000]
# initiate DeepGraph
cpg = dg.DeepGraph(cpv)
# create edges
cpg.create_edges(connectors=[cp_node_intersection,
cp_intersection_strength],
no_transfer_rs=['intsec_card'],
logfile='create_cpe',
step_size=1e7)
Since no selection of edges has taken place, the number of edges should
be cpg.n*(cpg.n-1)/2
cpg
<DeepGraph object, with n=5000 node(s) and m=12497500 edge(s) at 0x7f7a00aec128>
print(cpg.e)
intsec_strength
s t
1 2 0.018499
3 0.002457
4 0.000000
5 0.000000
6 0.000000
... ...
4997 4999 0.000000
5000 0.000000
4998 4999 0.000000
5000 0.000000
4999 5000 0.000000
[12497500 rows x 1 columns]
print(cpg.e.intsec_strength.value_counts())
0.000000 12481941
1.000000 787
0.111111 488
0.333333 481
0.500000 462
...
0.012346 1
0.158537 1
0.178082 1
0.658537 1
0.018809 1
Name: intsec_strength, dtype: int64
Hierarchically Agglomerate Clusters into Families¶
Based on the above measure of spatial overlap between clusters, we now perform an agglomerative, hierarchical clustering of the spatio-temporal clusters into regionally coherent families.
from scipy.cluster.hierarchy import linkage, fcluster
# create condensed distance matrix
dv = 1 - cpg.e.intsec_strength.values
del cpg.e
# create linkage matrix
lm = linkage(dv, method='average', metric='euclidean')
del dv
# form flat clusters and append their labels to cpv
cpv['F'] = fcluster(lm, 1000, criterion='maxclust')
del lm
# relabel families by size
f = cpv['F'].value_counts().index.values
fdic = {j: i for i, j in enumerate(f)}
cpv['F'] = cpv['F'].apply(lambda x: fdic[x])
Let’s see how many clusters there are in the families
print(cpv['F'].value_counts())
0 79
1 76
2 74
3 56
4 52
..
502 1
498 1
494 1
490 1
997 1
Name: F, dtype: int64
Create a “Raster Plot” of Families¶
Let’s plot the clusters of the largest 10 families in a raster-like boxplot, by means of the plot_rects_label_numeric method
cpgt = dg.DeepGraph(cpg.v[cpg.v.F <= 10])
obj = cpgt.plot_rects_label_numeric('F', 'time_amin', 'time_amax',
colors=np.log(cpgt.v.vol_sum.values))
obj['ax'].set_xlabel('time', fontsize=20)
obj['ax'].set_ylabel('family', fontsize=20)
obj['ax'].grid()
Create and Plot Informative (Intersection) Partitions¶
In this last section, we create some useful (intersection) partitions of the deep graph, which we then use to create some plots.
Geographical Locations¶
# how many components have hit a certain
# geographical location (discarding singular cps)
def count(cp):
return len(set(cp[cp != 0]))
# feature functions, will be applied to each g_id
feature_funcs = {'cp': [count],
'vol': [np.sum],
'lat': np.min,
'lon': np.min}
gv = g.partition_nodes('g_id', feature_funcs)
gv.rename(columns={'lat_amin': 'lat',
'lon_amin': 'lon'}, inplace=True)
print(gv)
n_nodes cp_count lat vol_sum lon
g_id
0 2 1 -10.125 10142 -125.125
1 2 1 -9.875 8716 -125.125
2 2 0 -9.625 4372 -125.125
3 2 2 -9.375 5310 -125.125
4 2 2 -9.125 6409 -125.125
... ... ... ... ... ...
115618 2 1 48.875 14319 5.125
115619 1 1 49.125 10129 5.125
115620 2 1 49.375 12826 5.125
115621 2 2 49.625 9117 5.125
115622 2 1 49.875 12101 5.125
[115623 rows x 5 columns]
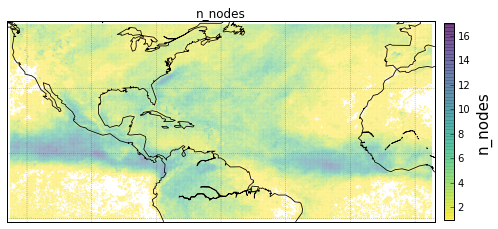
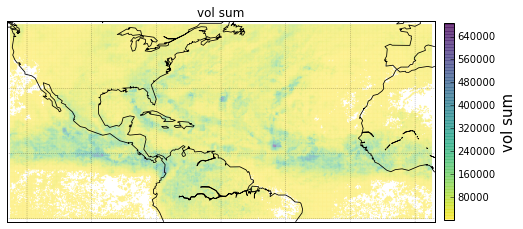
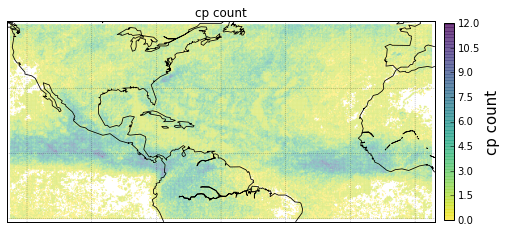
Plot GeoLocational Information¶
cols = {'n_nodes': gv.n_nodes,
'vol sum': gv.vol_sum,
'cp count': gv.cp_count}
for name, col in cols.items():
# for easy filtering, we create a new DeepGraph instance for
# each component
gt = dg.DeepGraph(gv)
# configure map projection
kwds_basemap = {'llcrnrlon': v.lon.min() - 1,
'urcrnrlon': v.lon.max() + 1,
'llcrnrlat': v.lat.min() - 1,
'urcrnrlat': v.lat.max() + 1}
# configure scatter plots
kwds_scatter = {'s': 1,
'c': col.values,
'cmap': 'viridis_r',
'alpha': .5,
'edgecolors': 'none'}
# create scatter plot on map
obj = gt.plot_map(lon='lon', lat='lat',
kwds_basemap=kwds_basemap,
kwds_scatter=kwds_scatter)
# configure plots
obj['m'].drawcoastlines(linewidth=.8)
obj['m'].drawparallels(range(-50, 50, 20), linewidth=.2)
obj['m'].drawmeridians(range(0, 360, 20), linewidth=.2)
obj['ax'].set_title(name)
# colorbar
cb = obj['fig'].colorbar(obj['pc'], fraction=.022, pad=.02)
cb.set_label('{}'.format(name), fontsize=15)
Geographical Locations and Families¶
In order to create the intersection partition of geographical locations
and families, we first need to append a family membership column to
v
# create F col
v['F'] = np.ones(len(v), dtype=int) * -1
gcpv = cpv.groupby('F')
it = gcpv.apply(lambda x: x.index.values)
for F in range(len(it)):
cp_index = v.cp.isin(it.iloc[F])
v.loc[cp_index, 'F'] = F
Then we create the intersection partition
# feature funcs
def n_cp_nodes(cp):
return len(cp.unique())
feature_funcs = {'vol': [np.sum],
'lat': np.min,
'lon': np.min,
'cp': n_cp_nodes}
# create family-g_id intersection graph
fgv = g.partition_nodes(['F', 'g_id'], feature_funcs=feature_funcs)
fgv.rename(columns={'lat_amin': 'lat',
'lon_amin': 'lon',
'cp_n_cp_nodes': 'n_cp_nodes'}, inplace=True)
which looks like this
print(fgv)
n_nodes n_cp_nodes lat vol_sum lon
F g_id
-1 0 2 2 -10.125 10142 -125.125
1 2 2 -9.875 8716 -125.125
2 2 1 -9.625 4372 -125.125
3 2 2 -9.375 5310 -125.125
4 2 2 -9.125 6409 -125.125
... ... ... ... ... ...
998 26685 1 1 -8.875 593 -93.625
26686 1 1 -8.625 411 -93.625
26887 1 1 -9.375 364 -93.375
26888 1 1 -9.125 478 -93.375
26889 1 1 -8.875 456 -93.375
[186903 rows x 5 columns]
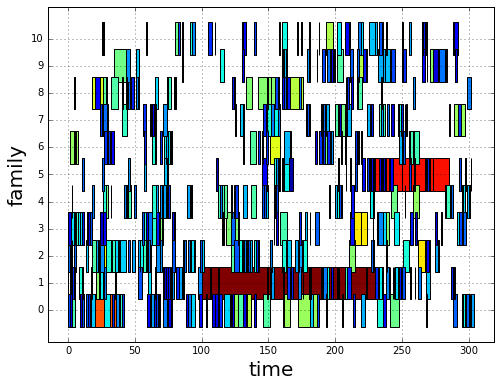
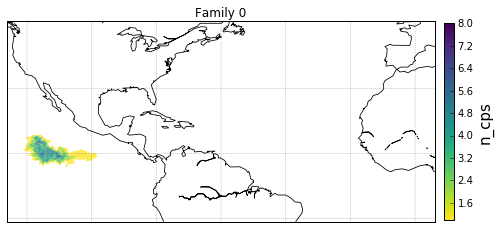
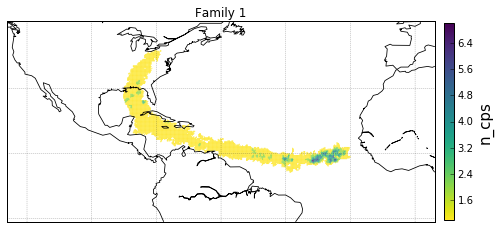
Plot Family Information¶
families = [0,1,2,3]
for F in families:
# for easy filtering, we create a new DeepGraph instance for
# each component
gt = dg.DeepGraph(fgv.loc[F])
# configure map projection
kwds_basemap = {'llcrnrlon': v.lon.min() - 1,
'urcrnrlon': v.lon.max() + 1,
'llcrnrlat': v.lat.min() - 1,
'urcrnrlat': v.lat.max() + 1}
# configure scatter plots
kwds_scatter = {'s': 1,
'c': gt.v.n_cp_nodes.values,
'cmap': 'viridis_r',
'edgecolors': 'none'}
# create scatter plot on map
obj = gt.plot_map(
lat='lat', lon='lon',
kwds_basemap=kwds_basemap, kwds_scatter=kwds_scatter)
# configure plots
obj['m'].drawcoastlines(linewidth=.8)
obj['m'].drawparallels(range(-50, 50, 20), linewidth=.2)
obj['m'].drawmeridians(range(0, 360, 20), linewidth=.2)
cb = obj['fig'].colorbar(obj['pc'], fraction=.022, pad=.02)
cb.set_label('n_cps', fontsize=15)
obj['ax'].set_title('Family {}'.format(F))
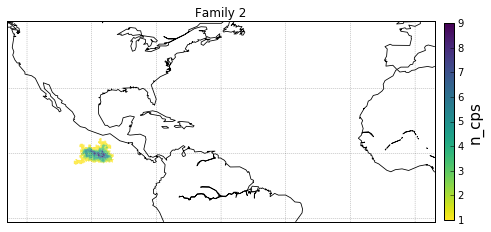
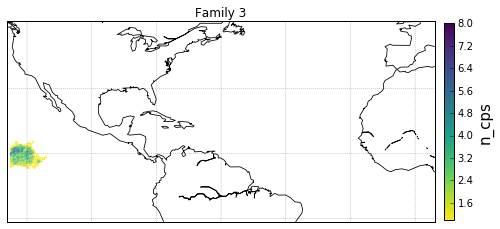
Geographical Locations and Components¶
# feature functions, will be applied on each [g_id, cp] group of g
feature_funcs = {'vol': [np.sum],
'lat': np.min,
'lon': np.min}
# create gcpv
gcpv = g.partition_nodes(['cp', 'g_id'], feature_funcs)
gcpv.rename(columns={'lat_amin': 'lat',
'lon_amin': 'lon'}, inplace=True)
print(gcpv)
n_nodes lat vol_sum lon
cp g_id
0 0 1 -10.125 5071 -125.125
1 1 -9.875 4415 -125.125
2 2 -9.625 4372 -125.125
6 3 -8.375 1026 -125.125
7 1 -8.125 594 -125.125
... ... ... ... ...
33167 112117 1 9.375 24618 0.625
33168 100613 1 6.625 11450 -13.625
100614 1 6.875 12706 -13.625
33169 98523 1 15.375 31057 -16.125
98524 1 15.625 15741 -16.125
[287301 rows x 4 columns]
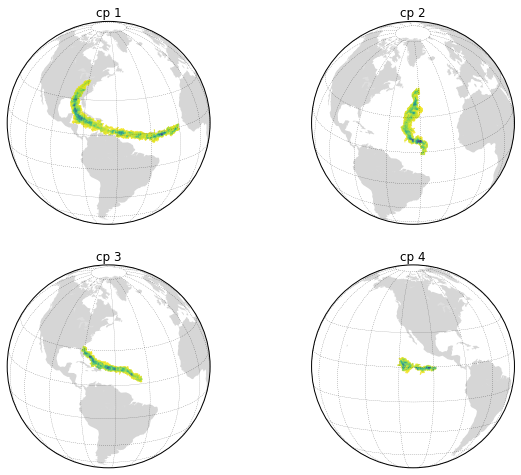
Plot Component Information¶
# select the components to plot
comps = [1, 2, 3, 4]
fig, axs = plt.subplots(2, 2, figsize=[10,8])
axs = axs.flatten()
for comp, ax in zip(comps, axs):
# for easy filtering, we create a new DeepGraph instance for
# each component
gt = dg.DeepGraph(gcpv[gcpv.index.get_level_values('cp') == comp])
# configure map projection
kwds_basemap = {'projection': 'ortho',
'lon_0': cpv.loc[comp].lon_mean,
'lat_0': cpv.loc[comp].lat_mean,
'resolution': 'c'}
# configure scatter plots
kwds_scatter = {'s': .5,
'c': gt.v.vol_sum.values,
'cmap': 'viridis_r',
'edgecolors': 'none'}
# create scatter plot on map
obj = gt.plot_map(lon='lon', lat='lat',
kwds_basemap=kwds_basemap,
kwds_scatter=kwds_scatter,
ax=ax)
# configure plots
obj['m'].fillcontinents(color='0.2', zorder=0, alpha=.2)
obj['m'].drawparallels(range(-50, 50, 20), linewidth=.2)
obj['m'].drawmeridians(range(0, 360, 20), linewidth=.2)
obj['ax'].set_title('cp {}'.format(comp))
